试卷说明:
考试时间为3小时,高低年组各有10道选择题和4道简答题。
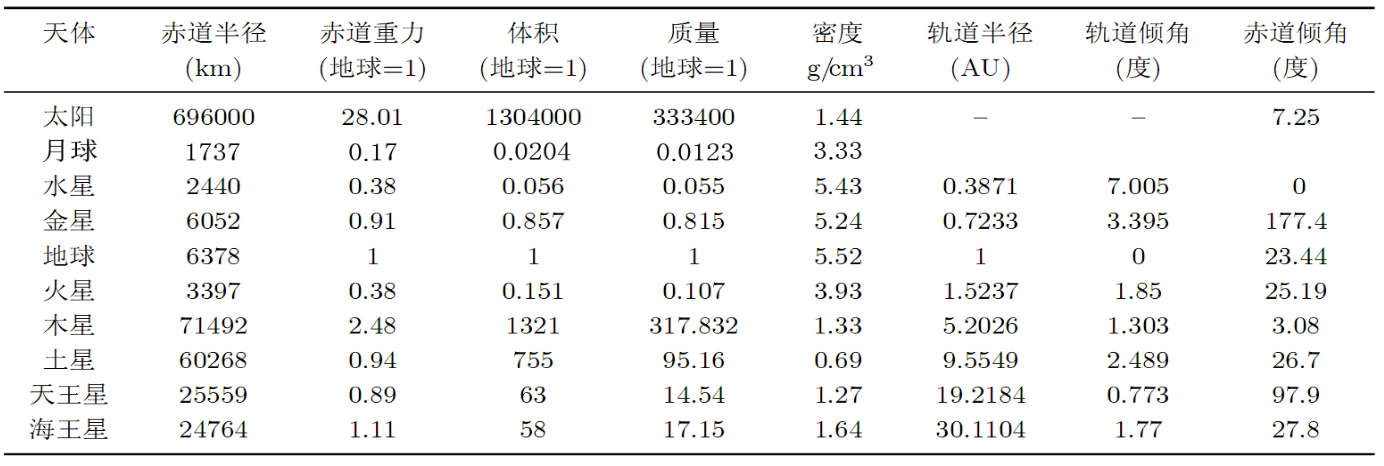
行星数据表
选择题
满分40分。每题选择一个最接近正确的答案,答对得4分,答错或多选得-4分,不选得0分。低年组答1~10题,高年组答4~13题。
1、( )下列哪个流星雨的源头可能不是彗星?
A、象限仪座流星雨 B、英仙座流星雨 C、双子座流星雨 D、猎户座流星雨
2、( )海王星最初是在哪个星座发现的?
A、宝瓶座 B、室女座 C、摩羯座 D、狮子座
3、( )南、北银极在什么星座(或哪两个星座方向最适合观测河外星系)?
A、玉夫座、后发座 B、天炉座、后发座 C、 玉夫座、室女座 D、凤凰座、室女座
4、( )下列星系中离银河系最近的河外星系是?
A、仙女座大星系 B、大麦云 C、小麦云 D、大犬座不规则星系
5、( )每年三月下旬左右爱好者都会尝试“梅西叶马拉松”观测。下列梅西叶天体中,一般作为马拉松观测起始的目标是哪个?
A、M45 B、M60 C、M1 D、M73
6、( )木卫一距木星的平均距离为4.22×105km,它绕木星的公转周期为1.77天,估计木星的质量(以地球质量为单位)。
A、120 B、 230 C 、320 D、 480
7、( )太阳系内最大的天然卫星是?
A、木卫三 B、 海卫二 C、月球 D、 土卫六
8、( )两颗星有同样的绝对星等,但一颗星比另一颗的距离远1000倍,它们的视星等差是多少?
A、15 B、999 C 、6.5 D、30.6
9、( )我们的太阳是一颗什么样的恒星?
A、红巨星 B、主序星 C、白矮星 D、黄巨星
10、( )哪一颗天体不是矮行星?
A、谷神星 B、冥王星 C、阋神星(Eris)D、1992QB1
11、( )外行星从合日到冲的亮度变化为0.85个星等。估计合日到冲经过多少天?行星轨道可以视为圆形且位于黄道面。
A、200天 B 、100天 C、 248天 D 、387天
12、( )一年中地球上可能发生8次日月食吗?
A、完全不可能 B、在地球上的某些特殊地方可能 C、在某些特别年份可能 D、在特别年份地球上某些特殊地方可能
13、( )氢分子的平均速度可以用公式计算,其中T为绝对温度。估计在月球正午时(温度取为120摄氏度),是否会有大量氢分子飞离月球?
A、完全没有 B、仅有少量 C、确实有大量 D、还需要知道其他数据才能确定答案
答案:A A A D A C A A B D A A C
简答题
共60分。每题15分,只写公式或只给出最后答案的均不能得满分。低年组答14~17题,高年组答15~18题。
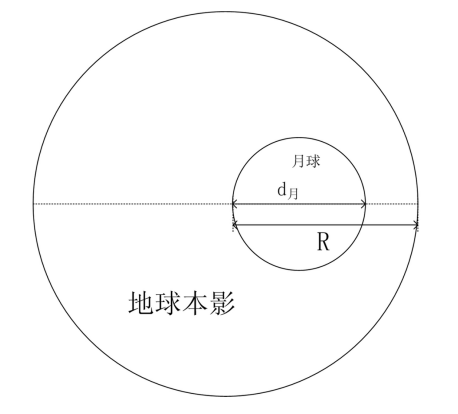
14、(低年组)【月食的食分】
月食的食分是体现月面进入地球本影程度的量,具体计算方法如图(图为月食食甚时的示意图)。假定月面和地球本影都是正圆,那么定义月食食分为R与月面直径d 月的比值,其中R为月面与地球本影两圆心连线上,经过月面边缘、地影边缘的最小距离。月球绕地球的公转轨道为椭圆,两者距离变化范围为360000~400000km。求月全食食分的理论最大值。(日地距离取1.5×108km)
参考答案:
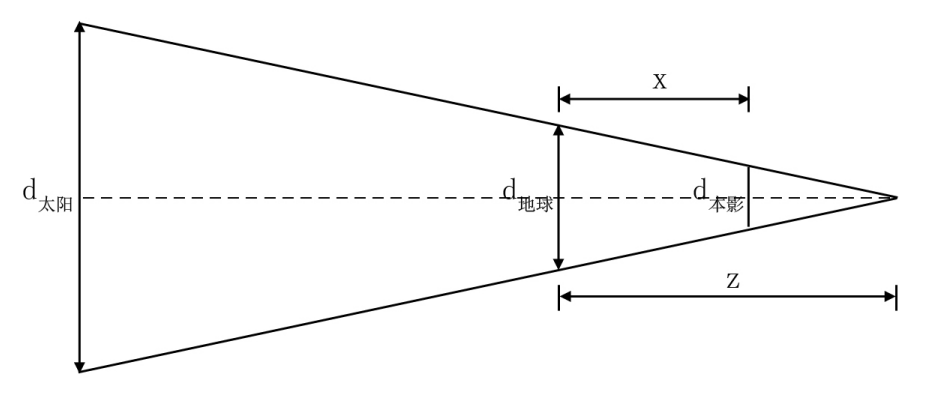
如图所示,我们先来计算地球本影的直径d本影。根据相似三角形原理:
z/(z+1.5×108)=d地球/d太阳,d本影/d地球=(z-x)/z
代入已知数据可以求出:
z=1.3725×106 km,d本影=12746-9.2867×10-3 x (1)
从题干所给出的图可知,当食甚时月心与地球本影中心重合时,月食食分最大。此时从地球上看,地影的角直径为:d本影/x弧度,月球的角直径为:d月球/x弧度,因此食分为:
R/d月球=(d本影/2+d月球/2)/d月球 (2)
地月距离(x)越小,食分越大,取x=360000 km,代入月球直径数据,即可根据(1)、(2)式求出月食的最大食分为:1.8525。
15、(高低年组共用)【兴隆观测】
时角(记为t)是指过北天极、天体、南天极的大圆与子午圈(即过北天极、天顶、南天极的大圆)的夹角,通常以0h~±12h来计量,向东为负,向西为正。天体的赤经(α)、时角(t)与当时的地方恒星时(S)满足以下关系:
S=α+t
假设我们在兴隆观测站观测天体A(α=18h, δ= +23 º30′)和天体B(α=05h, δ= -23 º30′),请问:
1)估算在一年里的哪一天,天体B会在当地时间子夜上中天?
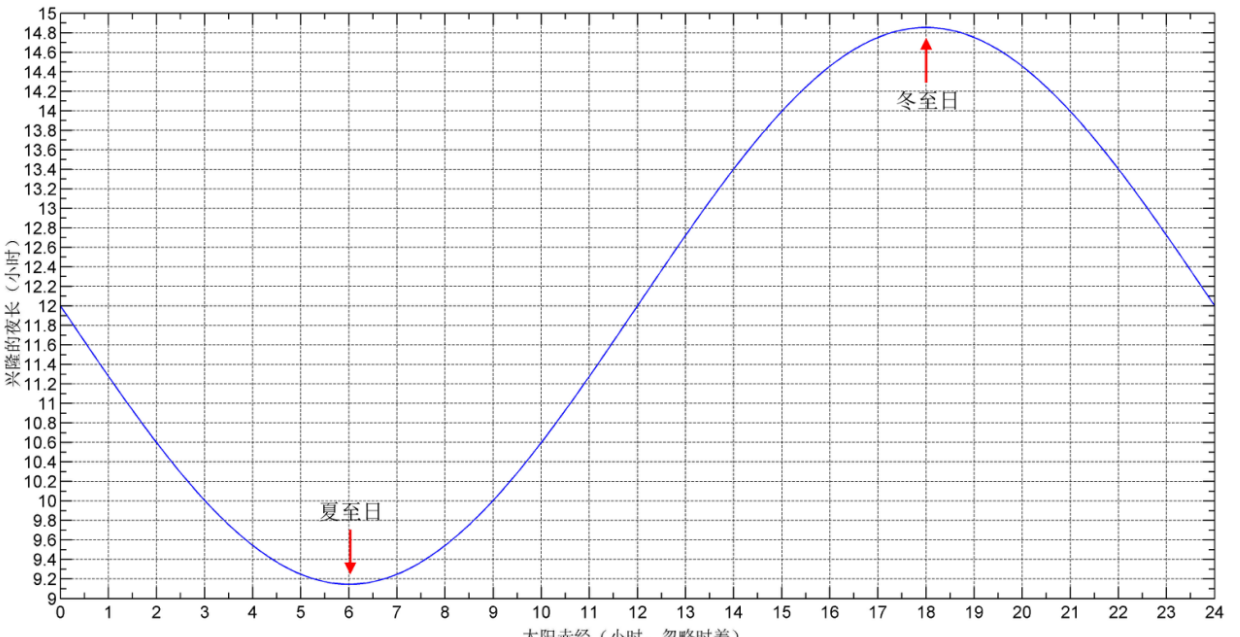
2)(仅低年组)下图是兴隆在一年中黑夜长度的示意图(忽略了时差效应)。如果我们想在太阳落山后半小时进行观测,估计在一年中的哪段时间里,在观测时刻能够看到A和B都位于地平线以上?给出大致的日期范围。
- (仅高年组)下图是兴隆在一年中黑夜长度的示意图(忽略了时差效应)。假如太阳落山后半小时至升起前半小时我们都能进行观测,估计在一年的哪段时间可以在晚上观测到A和B同时位于地平线以上?给出大致的日期范围。
解答:
1)B的赤经为05h,可知它上中天时的地方恒星时为S=05h,此时的地方平时为0h。我们知道秋分日(9月23日左右)地方平时0h的地方恒星时也为0h,此后恒星时每天比平时快4分钟左右,于是可知经过2月15天,地方平时为0h时的恒星时为05h,即所求日期为12月7日左右。
2)(仅低年组)A的赤纬与夏至日的太阳(αʘ=90°)相当,B的赤纬与冬至日的太阳(αʘ=270°)相当,它们每天从落下到升起所经历的时间可以从图中读出,A约为9.2小时,B约为14.8小时。假设某日的夜长为Tʘ小时,太阳的赤纬为αʘ,则当太阳下山后半小时,它的时角为:
tʘ=(24-Tʘ)/2+0.5=12.5h-Tʘ/2
要想当晚能观测这两个天体,有两种可能性:
(1)此时,B已经升起而A尚未落下。根据αʘ+tʘ=α1+t1=α2+t2可知:
tA=αʘ+tʘ-αA <(24-9.2)/2=7.4h
tB=αʘ+tʘ-αB >-(24-14.8)/2=-4.6h
带入数据并对上式进行整理可得:
-0.1h(亦即24h-0.1h=23.9h)<αʘ+12.5h-Tʘ/2<25.9h
从图上找出满足上式的αʘ的范围大致为:
18.8h<αʘ<20.5h
所对应的日期大致为:2月1(±5)日~2月27(±5)日。
(2)此时,A已经升起而B尚未落下,即
tA=αʘ+tʘ-αA >-(24-9.2)/2=-7.4h
tB=αʘ+tʘ-αB <(24-14.8)/2=4.6h
也就是:10.6h<αʘ+tʘ<9.6h,这种情况不可能发生。
3)(仅高年组)A的赤纬与夏至日的太阳(αʘ=90°)相当,B的赤纬与冬至日的太阳(αʘ=270°)相当,它们每天从落下到升起所经历的时间可以从图中读出,A约为9.2小时,B约为14.8小时。假设某日的夜长为Tʘ小时,太阳的赤纬为αʘ,则当太阳下山后半小时,它的时角为:
tʘ1=(24-Tʘ)/2+0.5=12.5h-Tʘ/2
太阳升起前半小时,它的时角为:
tʘ2=-(24-Tʘ)/2-0.5=-12.5h+Tʘ/2
为了计算方便,我们把时角重新定义为从子午圈自东向西起量,取值为0h~24h,以免出现负值。则日落后半小时到日出前半小时太阳的时角范围为:
12.5h-Tʘ/2≤tʘ≤11.5h+Tʘ/2 (1)
要想当晚能观测这两个天体,有两种可能性:
(1)在12.5h-Tʘ/2≤tʘ≤11.5h+Tʘ/2的这段时间里,B已经升起而A尚未落下。根据αʘ+tʘ=α1+t1=α2+t2可知:
tA=αʘ+tʘ-αA <(24-9.2)/2=7.4h
tB=αʘ+tʘ-αB >-(24-14.8)/2=-4.6h
带入数据并对上式进行整理可得:
-0.1h(亦即24h-0.1h=23.9h)<αʘ+tʘ<25.9h (2)
又根据(1)式可知αʘ+tʘ的取值范围为:
αʘ+12.5h-Tʘ/2≤αʘ+tʘ≤αʘ+11.5h+Tʘ/2
所以,当αʘ+tʘ的最大值(即αʘ+11.5h+Tʘ/2)小于23.9h或者αʘ+tʘ的最小值(即αʘ+12.5h-Tʘ/2)大于25.9h时,肯定不可能同时观测到二者,而其他时候则可以。
我们可以从图上大致读出:
αʘ+11.5h+Tʘ/2≤23.9h时,αʘ≤7.7h;αʘ+12.5h-Tʘ/2≥25.9h时,αʘ≥20.5
所以,能同时看到二者时,太阳赤经应满足:
7.7h<αʘ<20.5h
所对应的日期大致为:7月18(±5)日~2月27(±5)日。注意不是2月27(±5)日~7月18(±5)日!
(2)A已经升起而B尚未落下。
tA=αʘ+tʘ-αA ≥-(24-9.2)/2=-7.4h
tB=αʘ+tʘ-αB ≤(24-14.8)/2=4.6h
即:10.6h≤αʘ+tʘ≤9.6h,这种情况不可能发生。
注:由于考试时试题的题干上写的是“估计在一年的哪段时间可以在晚上观测到A和B同时位于地平线上”,易引起歧义,本题的2)和3)问没有计入最终成绩。
16、(高低年组共用)【星座】。列出你所知道的有关武仙座的尽可能多的信息。比如:在天球中的位置,有关的神话传说,星座大致的形状(画图),在某个特定日期或者月份升起和落下的大致时间,该星座里著名的亮星和特殊天体,尽可能多的相邻的星座名称,等等。
答案:略
17、(高低年组共用)【小行星的有效直径】。
小行星等天体的反照率可以简单地理解为它反射的光流量(F1)与接收到的入射光流量(F2)之比:p=F1/F2,F的单位为J/s。对小行星这样的太阳系内天体,天文学家定义其绝对星等(记作H)为:距离小行星1AU处的观测者,观测到小行星在距离太阳1AU时的视星等(假设观测者正对着反光面)。
- 我们知道小行星接收到的太阳辐射流量正比于它的(垂直于辐射方向的)截面积。天文研究中常常先假定所研究的小行星是球形,然后可以根据p和H求出它的直径D,D称为小行星的“有效直径”。推导求D的公式,D以km为单位。
- 小行星2009 WZ104是一颗可能对地球造成威胁的近地小行星,天文学家测得它的绝对星等H=20.52等,反照率可能在16~0.21之间,密度为2.7g/cm3。如果它撞上地球,所释放的能量至少相当于发生多少次9级地震?已知9级地震释放的能量约为:1.0×1017 J。
参考答案:
1)设在距离太阳1AU处,太阳的辐射流量为F0(J/s/m2),则直径为D米的小行星在此处接收到的太阳辐射流量为:
F2=F0×πD2/4 (J/s)
它反射的辐射流量为:
F1=p×F2=p×F0×πD2/4 (J/s)
太阳在1AU处的视星等为:
vs=-2.5lgF0=-26.7等,
而距离太阳1AU的小行星在1AU处的视星等(即绝对星等)为:
H=-2.5lg[F1/(π×1AU2)]
注意,由于小行星只有一半反射阳光,上式中不应是F1/(4π×1AU2),只是具体计算需要用到积分,通常中学生容易想到的是F1/(2π×1AU2),也可算作正确答案。
二者相比较,有:
H-vs=-2.5lg[(F1/(π×1AU2)/F0]
代入数据可知:
D=2×10-0.2(H+26.7)/p0.5 AU=1329×10-0.2H/p0.5 km
2)将H=20.52,p=0.16~0.21代入上式,可以求出:D=227~261 m。其质量至少为:M=4/3π×(22700/2)3×2.7g=1.65×1010 kg。它撞上地球时的速度至少为地球上的逃逸速度,即v=11.2 km/s。因此它撞地球时释放的能量至少为:
E=1/2Mv2=1.65×1010/2×1.25×108 J=1.03×1018 J≈10次九级地震
18、(高年组)【类地行星】。
截止到2011年2月1日,根据“凌星法”搜寻类地行星的“开普勒”空间望远镜已经搜索了153196颗类太阳恒星,发现了千余颗系外行星。根据这些观测数据,我们可以总结出关于系外行星的以下统计规律:
A)半径大于r的行星在所有0.5R地球≤r≤4R地球的行星中所占的比例为:
P(R行星>r)=(r/0.5)-1.45,当0.5R地球≤r≤4R地球时成立
B)约化轨道半长径大于s的行星在所有0.2 AU≤s≤1.5 AU的行星中所占的比例为:
P(s行星>s)=(s/0.2)-2.16,当0.2 AU≤s≤1.5 AU时成立
其中,称为“约化半长径”(scaled semimajor axis),其单位为AU,这里的a为行星公转轨道的半长径(以AU为单位),L为母恒星的光度(以太阳光度为单位)。
观测表明,这153196颗类太阳恒星周围的行星中,存在凌星现象(因而能被“开普勒”发现)并且满足2R地球≤r≤4R地球且0.2 AU≤s≤0.5 AU的行星,共有94颗。
如果我们对类地行星做如下定义:
A)行星半径满足0.8R地球≤r≤2R地球
B)行星位于恒星的可居住带内,可居住带的定义为:0.95 AU≤s≤1.37 AU。
请根据以上信息计算:
1)从理论上看,这153196颗类太阳恒星周围的行星中,可能被“开普勒”找到的类地行星大约有多少颗?
2)这153196颗类太阳恒星周围的行星中,总共应该有多少颗类地行星?假设恒星-行星系统的轨道平面与“开普勒”的视线方向的夹角i是随机分布的。
3)在银河系中,像太阳这样的恒星周围存在着和地球一样宜居的行星的概率大概为多少?
参考答案:
1)“开普勒”找到的类地行星的数目记为NT。我们把它和已被“开普勒”发现的满足2R地球≤r≤4R地球并且0.2 AU≤s≤0.5 AU的NK颗行星进行比较:
NT/NK=P(0.8R地球≤r≤2R地球)/P(2R地球≤r≤4R地球)×P(0.95 AU≤s≤1.37 AU)/P(0.2 AU≤s≤0.5 AU)
=[(2/0.5)-1.45-(0.8/0.5)-1.45]/[(4/0.5)-1.45-(2/0.5)-1.45]×
[(1.37/0.2)-2.16-(0.95/0.2)-2.16]/[(0.5/0.2)-2.16-(0.2/0.2)-2.16]=0.0954
带入NK=94颗,可以求出:NT=94×0.0954=8.97=9颗。
2)能观察到凌星现象的行星轨道面倾角i应该满足:
-atan(R*/a)<i<atan(R*/a)
其中a为行星的轨道半长径,R*为恒星半径,对本题涉及到的类地恒星而言,可以取为R⊙(R⊙=0.00465AU)。即对轨道半长径为a的行星而言,能通过凌星法发现的行星所占的比例为:
A=2×atan(R⊙/a)/(π)≈2R⊙/(aπ),R⊙/a<<1
对类太阳恒星周围的类地行星,其约化半长径可以取为s=a=1AU(或者为1.16AU),因此有:
A=2R⊙/(aπ)=0.00296(或者0.00255)
因此这153196颗类太阳恒星周围应该存在的类地行星数目为:
N1=9/A=3040颗(或3530颗)。
3)在银河系中,像太阳这样的恒星周围存在着和地球一样宜居的行星的概率大概为:N1/153196≈2%~2.3%。即每1000颗类太阳恒星周围就有2颗左右和地球类似的行星,而实际上,更科学地分析“开普勒”数据后,天文学家给出的结论是1.4%~2.7%。这一概率大大高于此前人们的估计值,因此地外文明存在的可能性也会大大提高。